Árbol de Expansión Mínima sujeto a restricciones de flujo

Agustín García Romero
ITESM. Paseo de la Reforma, Lomas de Cuernavaca.
Cuernavaca, Mor
E-Mail: [email protected]
http://www.mor.itesm.mx/~al374654

Marzo 1999

Abstract

Se explica paso a paso un ejemplo de cómo trabaja el algoritmo.

Uno de los algoritmos que nos permiten encontrar el Árbol de Expansión Mínima -AEM- es conocido como el Algoritmo de Prim, el cual construye un árbol a partir de la adición iterativa de arcos hasta que el AEM es obtenido. En cada iteración se agrega el arco de costo mímimo que no complete un ciclo en el árbol actual.

ENTRADA:

Un grafo conectado, con costos de conexión definidos entre los nodos, los cuales están numerados desde 1...n, y un nodo inicial s.

Si (i,j) es un arco, w(i,j) es igual al peso de (i,j); si (i,j) no es un arco, w(i,j) es igual a � (un valor mayor que cualquiera de los pesos).

SALIDA:

El conjunto de los arcos E en un AEM.[]

procedure prim(w,n,s)

//v(i) = 1 si el vértice i ha sido agregado al AEM.

//v(i) = 0 si el vértice i no ha sido agregado al AEM.

for i = 1 to n do

v(i) = 0

//Agregar nodo al AEM

v(s) = 1

//Inicializar el conjunto de arcos E en vacío

E = �

//Insertar los n-1 arcos restantes al AEM

for i = 1 to n-1 do

      begin

      min = �

      for j = 1 to n do

if v(j) = 1 then //j es un nodo en AEM

      for k = 1 to n do

if v(k) = = 0 and w(j,k) < min then

      begin

add_vertex = k

e = (j,k)

min = w(j,k)

      end

//Poner nodo y arco en AEM

v(add_vertex) = 1

E = E�{e}

end

return E

end prim

0.1  Ejemplo

Obtener el AEM -sin restricciones- del grafo que se presenta en la figura

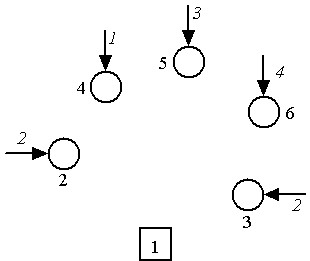
Grafo Sujeto a restricciones de flujo

Donde dicho grafo tiene la siguiente matriz de costos

c]lllllll	1	2	3	4	5	6
1	-	2	4	5	2	4
2	2	-	10	6	3	8
3	4	10	-	8	7	2
4	5	6	8	-	1	5
5	2	3	7	1	-	3
6	4	8	2	5	3	-

S = 1

E = { 0}

I = 1

E = { 0} U{ 1,2}

I = 2

E = { 0} U{ 1,2} U{ 1,5}

I = 3

E = { 0} U{ 1,2} U{ 1,5}U{ 5,4}

I = 4

E = { 0} U{ 1,2} U{ 1,5}U{ 5,4} U{ 5,6}

I=5

E = { 0} U{ 1,2} U{ 1,5}U{ 5,4} U{ 5,6} U{ 3,6}

[^c] = 0+2+2+1+3+2 = 10.

c]llllllV0	V1	V2	V3	V4	V5
1	1	1	1	1	1
0	1	1	1	1	1
0	0	0	0	0	1
0	0	0	1	1	1
0	0	1	1	1	1
0	0	0	0	1	1

I=1 min=�

c]llllllllJ	V(j)	K	V(k)	W(j,k)	min	add	e
1	1	1	1		�
		2	0	2	2	(1,2)	2
		3	0	4
		4	0	5
		5	0	2
		6	0	4
2	0
:	:
6	0

I=2 min=�

c]llllllllJ	V(j)	K	V(k)	W(j,k)	min	add	e
1	1	1	1		�
		2	1		�
		3	0	4	4	3	(1,3)
		4	0	5
		5	0	2	2	5	(1,5)
		6	0	4	2
2	1	1	1		2
		2	1		2
		3	0	10	2
		4	0	6	2
		5	0	3	2
		6	0	8	2
3	0
:	:
6	0

I=3 min=�

c]llllllllJ	V(j)	K	V(k)	W(j,k)	min	add	e
1	1	1	1		�
		2	1		�
		3	0	4	4	3	(1,3)
		4	0	5
		5	1
		6	0	4
2	1	1	1
		2	1
		3	0	10
		4	0	6
		5	0	3	3	5	(2,5)
		6	0	4
3	0
4	0
5	1	1	1
		2	1
		3	0	7
		4	0	1	1	4	(5,4)
		5	1	3
		6	0
6	0

I=4 min=�

c]llllllllJ	V(j)	K	V(k)	W(k,j)	min	add	e0
1	1	1	1		�
		2	1		�
		3	0	4	4	3	(1,3)
		4	1
		5	1
		6	0	4
2	1	1	1
		2	1
		3	0	10
		4	1
		5	1
		6	0	8
3	0
4	1	1	1
		2	1
		3	0	8
		4	1	�
		5	1
		6	0	5
5	1	1	1
		2	1
		3	0	7
		4	1
		5	1
		6	0	3	3	6	(5,6)
6	0

I=5 min=�

c]llllllllJ	V(j)	K	V(k)	W(k,j)	min	add	e
1	1	1	1		�
		2	1	4	4	3	(1,3)
		3	0
		4	1
		5	1
		0	1
2	1	1	1
		2	1
		3	0	10
		4	1
		5	1
		6	1
3	0
4	1	1	1
		2	1
		3	0	8
		4	1
		5	1
		6	1
5	1	1	1
		2	1
		3	0	7
		4	1
		5	1
		6	1
6	1	1	1
		2	1
		3	0	2	2	3	(6,3)
		4	1
		5	1
		6	1

Entoces, el AEM -sin restricciones- estará definido en la figura

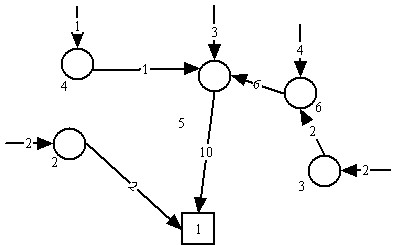
Solución del AEM sujeto a restricciones de capacidad

References

[]

Discrete Mathematics. Richard Johnsonbaugh. McMillan . 1993.

[]

Computer Communication Network Design and Analysis. Mischa Schwartz. Prentice Hall, 1977.